Rules
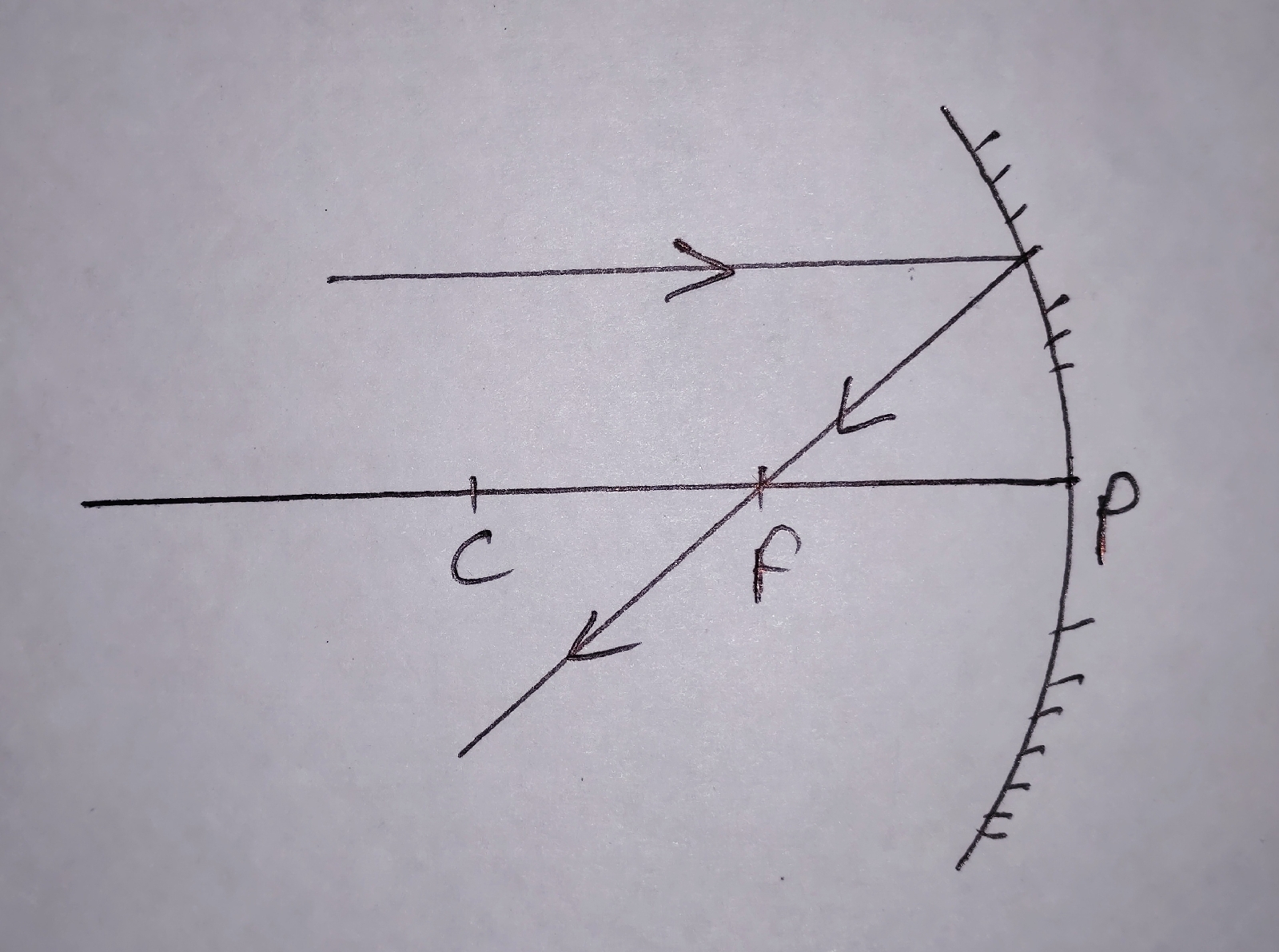
concave mirror
Rule 1
when light ray is moving parallel to the principal axis towards the mirror, it passes through the principal focus 'F' after reflection.
Rule 2
when light ray passes through the principal focus 'F', it goes parallel to the principal axis after reflection.
Rule 3
when light ray is incident on the pole of the mirror, it simply reflects from the pole.
Rule 4
when light ray passes through the centre of curvature 'C', it bounces back on its initial path.
convex mirror
Rule 1
when light ray is moving parallel to the principal axis towards the mirror, it goes in opposite direction to the principal focus after reflection.
Rule 2
when light ray approaches towards the principal focus, it goes parallel to the principal axis after reflection.
Rule 4
when light ray approaches towards the centre of curvature, it bounces back on its initial path after reflection.
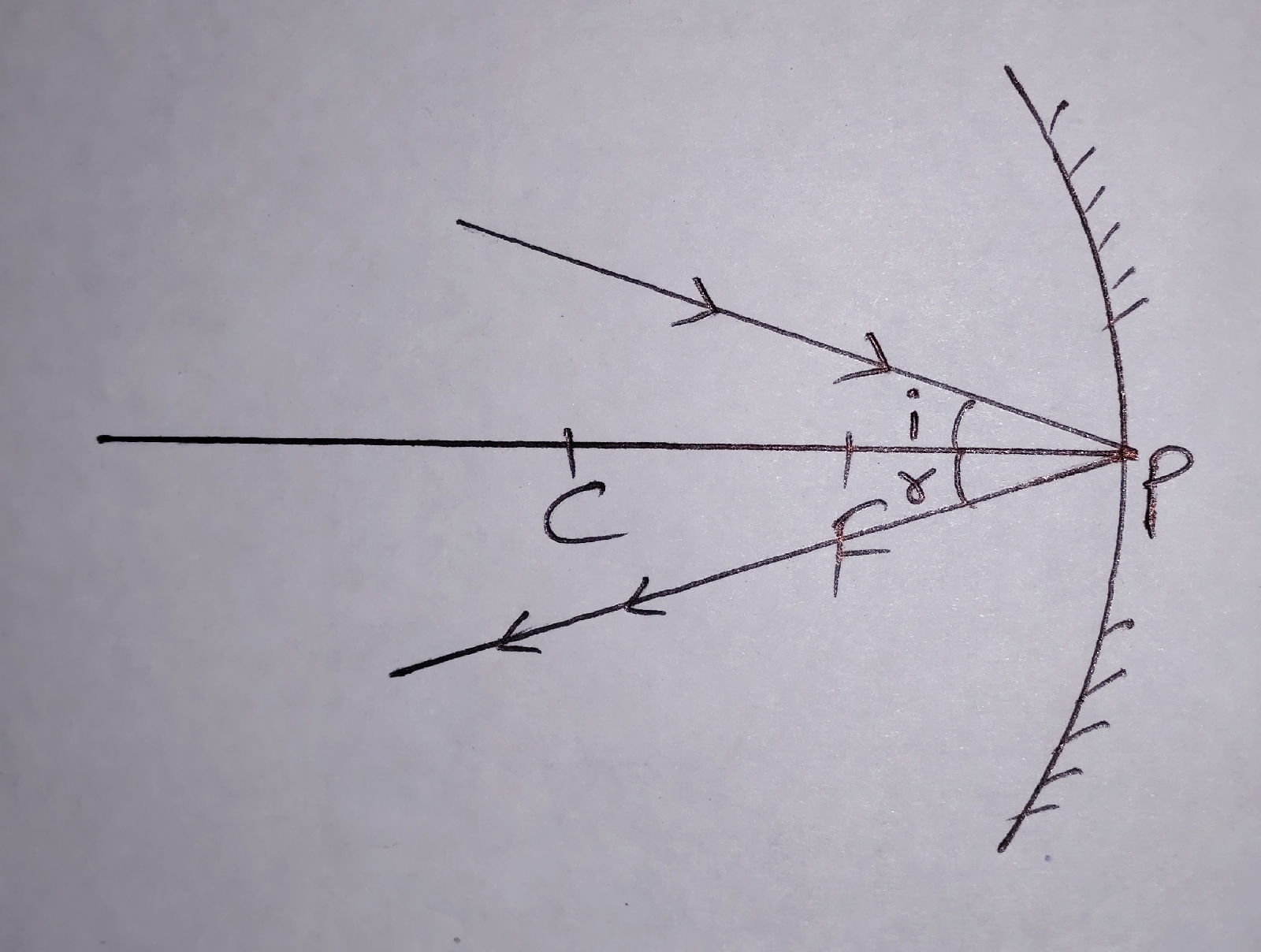
Mathematical Explaination (for curiosity only)
As we know, a tangent is perpendicular to the radius of a circle.
Draw a plane mirror tangent at the point of incidence of the spherical mirror (In this case, concave mirror). Now, draw a dotted line from C(before cutting, it was the centre of the hollow spherical glass) to the point of incidence.
As, CA is perpendicular to MN. Therefore, CA will become normal of the plane mirror as well as the spherical mirror because "A" is a common point for both mirrors.
So, we can that any line from C to the spherical surface of the mirror will be the normal to the mirror.
Now, rethink about Rule 4. Any light coming normal towards any mirror bounces back on its initial path.
For rule 1 and 2
let, angle i = θ
So, angle r = θ (law of reflection)
Draw AB perpendicular to CP
As, B and P are v. v. close. So, BP is v. v. small.
Therefore, BP is neglected.
Now, CB = CP = R (Radius of curvature)
FB = FP = f = R/2
for small angles-
tanθ = θ
(we have assumed that the parallel lines are close to each other)
In ∆ACF
CF = AF (approx.)
therefore, angle 1 = θ (isoceles triangle property)
Now, tan(angle 1) = AB/CB = AB/R ............(1)
tan(angle 2) = AB/FB = AB/R/2
tan(angle 2) = 2*AB/R ............(2)
from equation (1) & (2)
tan(angle 2) = 2*tanθ
therefore, angle 2 = 2θ
But, this is only possible when AD || BC.
therefore, AD || BC.
HENCE, PROVED. by www.advguruji.blogspot.com
concave mirror
Rule 1
when light ray is moving parallel to the principal axis towards the mirror, it passes through the principal focus 'F' after reflection.
Rule 2
when light ray passes through the principal focus 'F', it goes parallel to the principal axis after reflection.
Rule 3
when light ray is incident on the pole of the mirror, it simply reflects from the pole.
Rule 4
when light ray passes through the centre of curvature 'C', it bounces back on its initial path.
convex mirror
Rule 1
when light ray is moving parallel to the principal axis towards the mirror, it goes in opposite direction to the principal focus after reflection.
Rule 2
when light ray approaches towards the principal focus, it goes parallel to the principal axis after reflection.
Rule 4
when light ray approaches towards the centre of curvature, it bounces back on its initial path after reflection.
Mathematical Explaination (for curiosity only)
As we know, a tangent is perpendicular to the radius of a circle.
Draw a plane mirror tangent at the point of incidence of the spherical mirror (In this case, concave mirror). Now, draw a dotted line from C(before cutting, it was the centre of the hollow spherical glass) to the point of incidence.
As, CA is perpendicular to MN. Therefore, CA will become normal of the plane mirror as well as the spherical mirror because "A" is a common point for both mirrors.
So, we can that any line from C to the spherical surface of the mirror will be the normal to the mirror.
Now, rethink about Rule 4. Any light coming normal towards any mirror bounces back on its initial path.
For rule 1 and 2
let, angle i = θ
So, angle r = θ (law of reflection)
Draw AB perpendicular to CP
As, B and P are v. v. close. So, BP is v. v. small.
Therefore, BP is neglected.
Now, CB = CP = R (Radius of curvature)
FB = FP = f = R/2
for small angles-
tanθ = θ
(we have assumed that the parallel lines are close to each other)
In ∆ACF
CF = AF (approx.)
therefore, angle 1 = θ (isoceles triangle property)
Now, tan(angle 1) = AB/CB = AB/R ............(1)
tan(angle 2) = AB/FB = AB/R/2
tan(angle 2) = 2*AB/R ............(2)
from equation (1) & (2)
tan(angle 2) = 2*tanθ
therefore, angle 2 = 2θ
But, this is only possible when AD || BC.
therefore, AD || BC.
HENCE, PROVED. by www.advguruji.blogspot.com








Comments
Post a Comment